Семантический анализ веб-страниц
Перевод статьи “Semantic analysis of webpages with machine learning in Go”.
Я трачу довольно много времени на чтение статей в интернете. И подумал, что было бы неплохо написать небольшую программу, которая будет автоматически рекомендовать статьи, подходящие под мои интересы. Конечно, это очень обширная тема, но для начала я решил сконцентрироваться на основной проблеме: аналитики и классификации статей.
Для примера воспользуемся очень коротким текстом, будем считать его нашей статьей.
"the cunning creature ran around the canine"
Мы попытаемся использовать эту супер маленькую “статью” в качестве запроса для поиска аналогичных “статей” из набора других строк.
"The quick brown fox jumped over the lazy dog"
"hey diddle diddle, the cat and the fiddle"
"the fast cunning brown fox liked the slow canine dog "
"the little dog laughed to see such fun"
"and the dish ran away with the spoon"
Подходы, которые мы рассмотрим, могут работать с разными типами запросов. Это могут быть как статьи, так и просто короткие строки. Весь код будет доступен на github.
Частота термов
Один из основных подходов заключается в подсчете частоты встречаемости каждого слова(в нашем случае слово это “терм”) в каждой статье (статьи будем назвать “документами”). Затем документы можно представить как числовые векторы в которых хранятся значения частот повторения термов. В результате у нас будет большая матрица термов документов в которой каждый элемент tdi, j представлен частотой с которой терм ti встречается в документе dj. Ниже представлен пример такой матрицы. Для ее составления мы использовали наш набор статей.
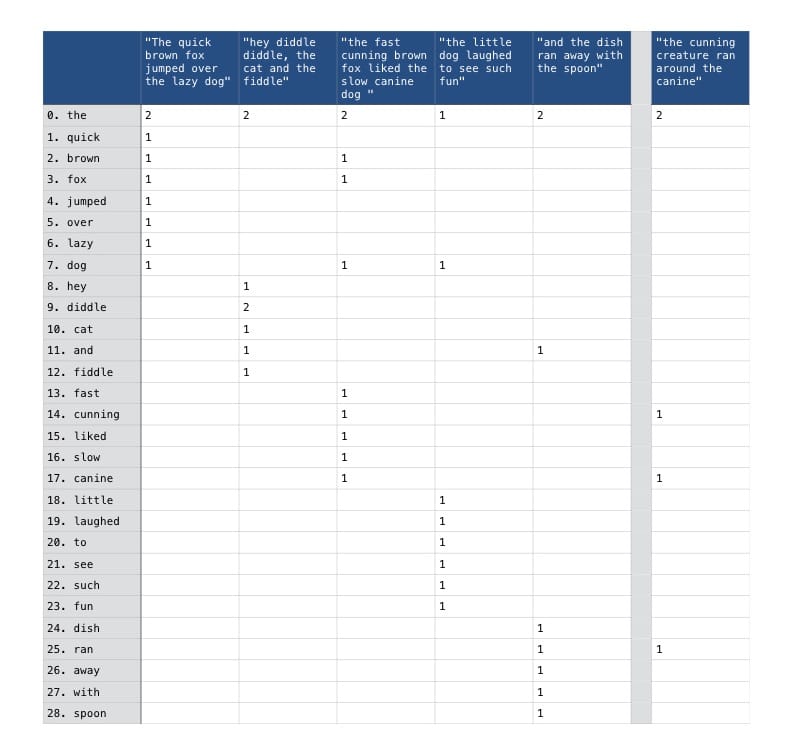
Значения нуля в нашей матрице показаны как пустые ячейки, что довольно сильно повышает читаемость таблички. Колонка справа показывает значения для статьи, которую мы использовали как запрос для поиска схожести, тут она показана для сравнения.
В нашем примере с матрицей сейчас не учитывается сходство слов и их последовательность. Мы просто считаем частоту с которой они встречаются в документе, независимо от того где они встречаются. Сразу заметно что в таком случае третья статья "the fast cunning brown fox liked the slow canine dog " имеет больше всего совпадений по термам с нашим запросом. Это сходство подтверждается сравнением косинусных сходство векторов из нашего набора с нашим запросом.
Косинусное сходство это математическая мера схожести двух числовых векторов. По сути, оно вычисляется через разницу между углами сравниваемых векторов. Для более полного понимания что такое косинусное сходство стоит почитать статью Кристиана Перона. Схожесть векторов выражается числом от 0 (полностью противоположные векторы) до 1 (абсолютно одинаковые векторы), чем ближе значение к 1 тем больше сходство. Сравнив наш запрос с каждым вектором мы получим результаты, показанные ниже:

По результатам видно, что наиболее близкая к нашему запросу статья как раз та самая "the fast cunning brown fox liked the slow canine dog".
Несмотря на то, что у нас получился неплохой результат, у нашего подхода есть несколько недостатков. Если внимательно посмотреть на результаты и нашу матрицу, то видно что второй документ "hey diddle diddle, the cat and the fiddle" имеет только одно совпадение с нашим запросом (the), а значение схожести аж 0.436436. Так происходит, потому что слово the встречается дважды и в запросе и в документе. Для сравнения, первый документ "The quick brown fox jumped over the lazy dog" семантически намного ближе к нашему запросу, но оценка схожести отличается очень незначительно. Мы должны исправить обе эти проблемы и начнем с первой: избавимся от слов, которые портят оценку, но не несут сематической нагрузки, такие как the, a, and и т.д.
TF-IDF (Term Frequency - Inverse Document Frequency)
Одни из вариантов решения этой проблемы - добавить вест нашим термам в зависимости от частоты их встречаемости в матрице. Чем чаше слово встречается в наших документах, тем меньше будет его вес. Соответственно, чем уникальнее слово, тем больше оно весит. Есть несколько алгоритмов для реализации такого подхода, но самый используемый это tf-idf. В tf-idf используется значение обратное частоте документов с термом умноженное на саму частоту терма из нашей матриц. В результате у нас будет tf-idf матрица с весами. Формула для расчета будет выглядеть так:
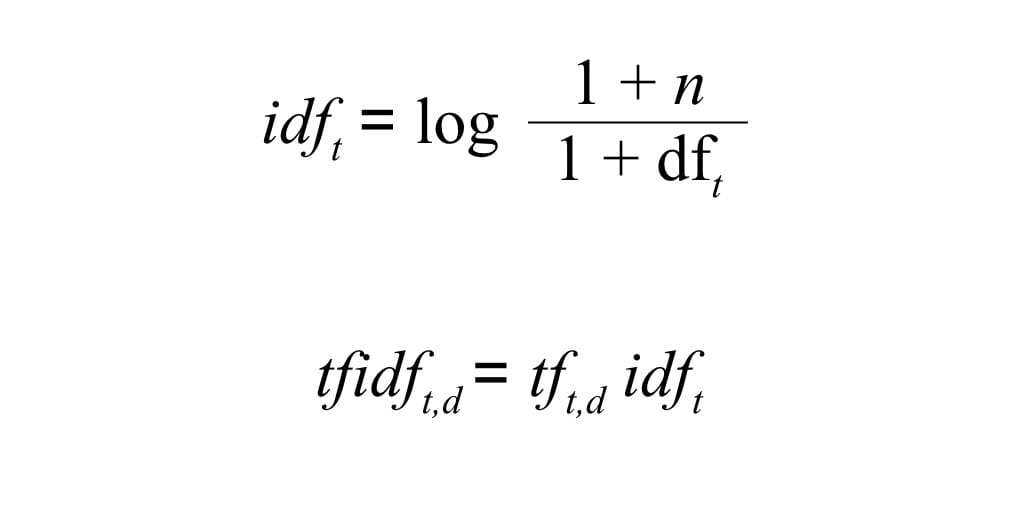
Где dft это частота документов, другими словами количество документов в которых встречается терм. n - количество документов в выборке. К обоим числам добавлены единицы, чтобы избежать проблем с делением на 0. При использовании такой формулы, вест термов, которые встречаются очень часто сразу во всех документах (например как the в нашей выборке), стремится к 0 и они как бы самоликвидируются.
И так, давайте посмотрим на новую матрицу, которую мы получили после использования tf-idf трансформации.
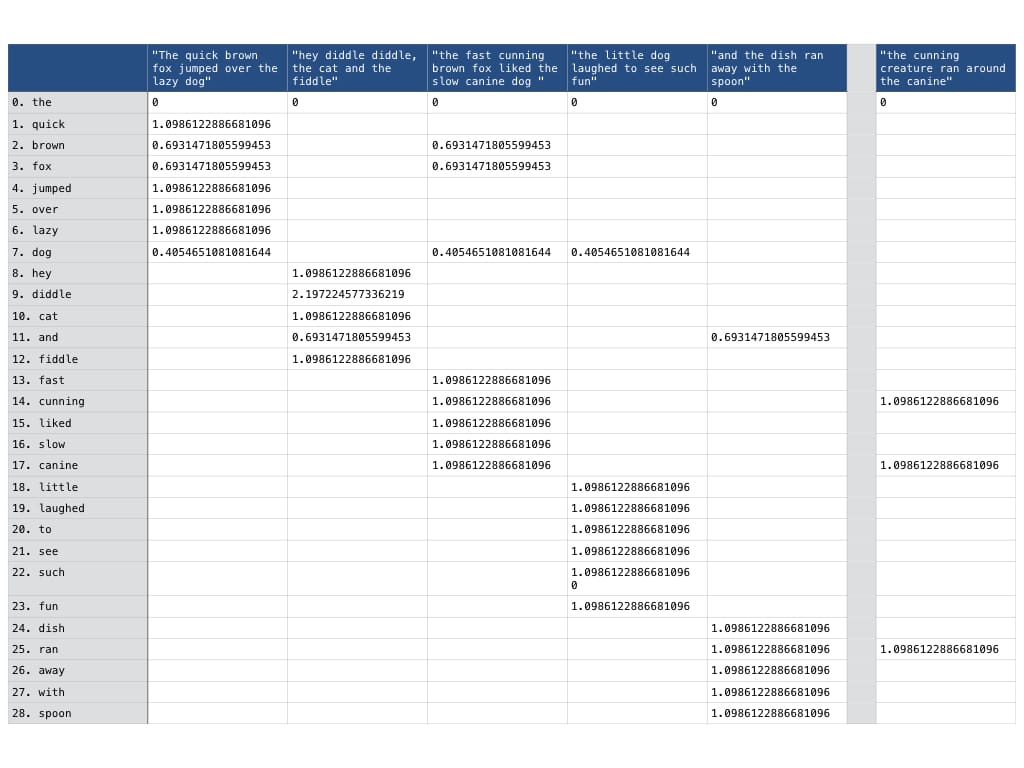
Как мы и рассчитывали, вес слова the практически сошел на нет и теперь равен 0 в нашей матрице. Не забывайте, что все преобразования, которые мы делаем над документами в нашей выборке должны также применятся и к нашему запросу, так чтобы мы могли их сравнить один к одному.
Теперь можно проверить, как использование tf-idf преобразования повлияло на косинусное сходство.

По этим результатам видно, что теперь на результаты влияют только те слова, которые есть исключительно в конкретном документе и в запросе. tf-idf преобразование удаляет лишний шум связанный с словами не несущими семантическую нагрузку и позволяет провести более точные вычисления.
Латентно-семантический анализ
Несмотря на то, что теперь у нас понятная оценка сходства, мы все еще не можем найти все семантически похожие документы. К примеру, первый документ The quick brown fox jumped over the lazy dog семантически очень похож на наш запрос - оба предложения про лис и собак. Тем не менее, при использовании tf-idf преобразование, оценка схожести косинусов этих векторов равна 0, а все потому что в этих предложениях нет совсем одинаковых слов(за исключением “мусорных”, у которы после tf-idf преобразования вес минимален). Так как же нам выделить семантический смысл, скрытый за частотой повторения термов? Использовать латентно-семантический анализ!
Латентно-семантический анализ (LSA или LSI)(оно же латентно-семантическое индексирование, когда речь идет про поиск информации) это способ поиска скрытых семантических атрибутов в набора документов на основе совместной встречаемости термов. Предполагается, что слова которые встречаются в документе вместе(с одинаковой частотой) несут определенную семантическую нагрузку и зависят от темы документа. Это имеет важное значение, когда в анализе участвуют разные слова имеющие одинаковое значение, когда в тексте есть синонимы. У нас появляется возможность сравнивать документы даже когда в них нет ни одного одинакового терма.
Латентно-семантический анализ базируется на математическом преобразовании, которое называется сингулярное разложение(SVD) и используется для уменьшения размерности нашей оригинальной матрицы. В результате сингулярного разложение мы получаем новую матрицу, которая максимально аппроксимирована к оригинальной матрице но с при этом значительно уменьшением размерность матрицы. Для более полного понимания математических основ SVD можете посмотреть мой код на github и/или походить по ссылкам в конце статьи. Преимущества получаемые после уменьшения размерности:
- После уменьшения размерности, теоретически, мы будем использовать меньше памяти.
- Мы избавимся от лишнего шума, и получим более правильные результаты.
- У нас появляется возможность учитывать скрытые семантические признаки, которые мы не могли использовать в случае сравнения только по термам.
Для нашего примера я буду использовать 2х размерную матрицу, так как для начало все равно стоит использовать не очень большую размерность, кроме того, такая матрица очень хорошо визуализируется. Как правило, при использовании LSA наилучшие результаты получаются при использовании около 100 значений. Давайте посмотрим как выглядит наша матрица после применения SVD.
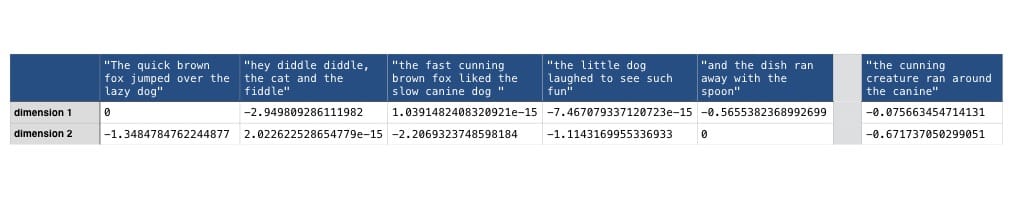
Раньше у нас была матрица с указанием значений по каждому терму, теперь осталось всего два измерения, значения в которых представляют наибольшие различия между документами. Нужно не забыть, что наш запрос нужно привести к такой же размерности, перед тем как сравнивать его с другими документами.
Так как теперь у нас каждый документ представлен всего в двух измерениях, его очень легко изобразить на графике в виде точки. Это поможет нам визуализировать определенные паттерны среди документов.
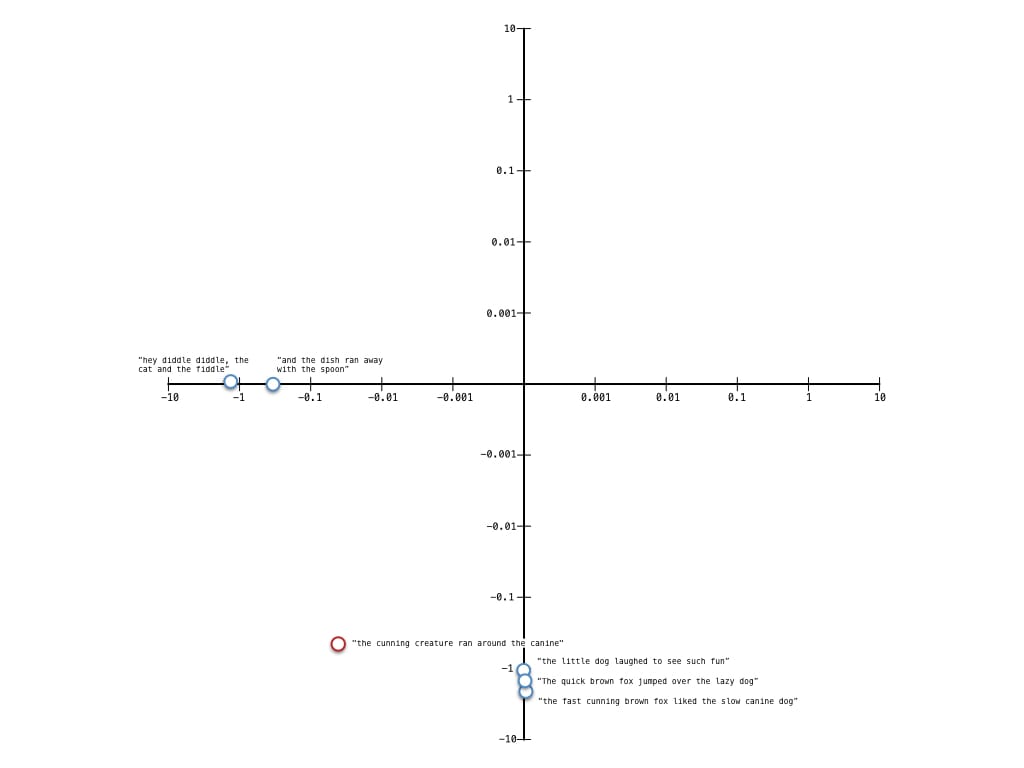
Внимательный читатель обратит внимание, что я использую логарифмическую шкалу по всем осям - это делает наш график более читаемым и мы можем глазами увидеть как наш запрос расположен относительно других документов. Глядя на график видно, что наши документы разделились на два основных кластера в двумерном пространстве. Некоторые имеют отношение к лисам и собакам, а некоторые нет. Кроме того, очень хорошо видно, что наш запрос ближе к тому кластеру, который как раз про собак и лис, собственно, именно так и должно быть. Давайте убедимся в этом, проверив косинусное сходство этих векторов.

Результаты проверки косинусного сходства подтверждают наши догадки на основе графиков. Так же, видно, что к нашему запросу "the cunning creature ran around the canine" больше всего подходит документ "The quick brown fox jumped over the lazy dog", несмотря на то, что нет никаких достаточно основательных общих термов. LSA также решает проблему семантической связи нашего запроса с лисами и собаками.
Реализация на Go
Я запрограммировал описанные в статье алгоритмы и опубликовал их на github. Реализация основана на разичных опубликованных вайт-пеперах и туториалах, сама структура позаимствована из питоновского проекта scikit-learn. Я привел небольшой пример как пользоваться моей библиотекой для расчета косунусного сходства между нашим запросом и документами из нашего набора, с использованием частот векторов, tf-idf преобразования и SVD факторизации.
1package main
2
3import (
4 "fmt"
5
6 "github.com/gonum/matrix/mat64"
7 "github.com/james-bowman/nlp"
8)
9
10func main() {
11 testCorpus := []string{
12 "The quick brown fox jumped over the lazy dog",
13 "hey diddle diddle, the cat and the fiddle",
14 "the fast cunning brown fox liked the slow canine dog ",
15 "the little dog laughed to see such fun",
16 "and the dish ran away with the spoon",
17 }
18
19 query := "the cunning creature ran around the canine"
20
21 vectoriser := nlp.NewCountVectoriser()
22 transformer := nlp.NewTfidfTransformer()
23
24 // указываем размерность k = 2
25 reducer := nlp.NewTruncatedSVD(2)
26
27 // Заполняем и преобразовываем набор документов в матрицу для
28 // для дальнейшей обработки
29 mat, _ := vectoriser.FitTransform(testCorpus...)
30
31 // Приводим наш запрос к такой же размерности -
32 // любой терм в запросе и не в оригинальных обучающих данных
33 // модели будет игнорироваться
34 queryMat, _ := vectoriser.Transform(query)
35 calcCosine(queryMat, mat, testCorpus, "Raw TF")
36
37 tfidfmat, _ := transformer.FitTransform(mat)
38 tfidfquery, _ := transformer.Transform(queryMat)
39 calcCosine(tfidfquery, tfidfmat, testCorpus, "TF-IDF")
40
41 lsi, _ := reducer.FitTransform(tfidfmat)
42 queryVector, _ := reducer.Transform(tfidfquery)
43 matched, score = calcCosine(queryVector, lsi, testCorpus, "LSA")
44}
45
46func calcCosine(queryVector *mat64.Dense, tdmat *mat64.Dense, corpus []string, name string) {
47 // Итерируемся по всем полученным векторам(колонкам) полученным после LSI
48 // и сравниваем с вектором нашего запроса. Схожесть векторов о зависит
49 // от угла между ними, это еще называется косинусной схожестью
50 _, docs := tdmat.Dims()
51
52 fmt.Printf("Comparing based on %s\n", name)
53
54 for i := 0; i < docs; i++ {
55 similarity := nlp.CosineSimilarity(queryVector.ColView(0), tdmat.ColView(i))
56 fmt.Printf("Comparing '%s' = %f\n", corpus[i], similarity)
57 }
58}
В результате
Мы рассмотрели работу с моделями документа для “добывания” некоторой информации о этих документах. Эти модели строятся одна поверх другой. Мы начали работу с документами, представляя их в виде векторов, в которых были записаны значения частот по каждому терму. Затем мы расширили эту модель, использовали tf-idf преобразование. С его помощью мы выяснили как использовать значения частот встречаемости термов не только в рамках одного документа, а с учетов всех документов для конкретного терма, что позволило избавится от “мусорных” слов. И в конце-концов мы применили латентно-семантический анализ и сингулярное разложение для вычленения семантического смыла предложения, скрытого за частотой встречаемости термов.
Я многому научился как за время реализации алгоритмов машинного обучения(и сопутствующей математики), так и приложений, которые используют эти алгоритмы. Я планирую реализовать много различных дополнений к моей библиотеке для расширения моих познаний в машинном обучении. Тем не менее, в этой библиотеке уже реализована LDA (Latent Dirichlet Allocation) для эффективного извлечения темы из документов. И эта библиотека уже может использоваться в алгоритмах классификации и кластеризации, таких как нахождение к-средних и типа того.
Если у вас есть опыт в использовании описанных мною алгоритмов или аналогичных, то приходите в комментарии и делитесь опытом.